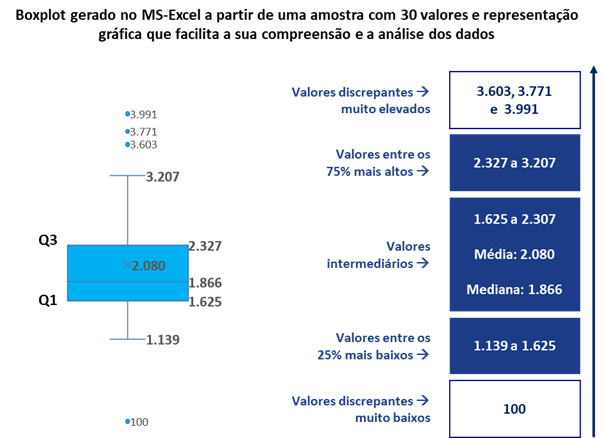
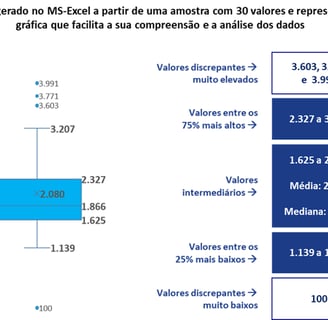
No exemplo apresentado, se fôssemos adotar apenas a média, nossa análise diria que os trabalhadores ganham em média R$ 2.080, mas com a utilização do boxplot é possível obtermos uma compreensão mais precisa dos salários dos trabalhadores do nosso exemplo. Apenas para ilustrar, há uma diferença considerável entre os valores mínimo e máximo encontrados, situação que a média não possibilita verificar.
Ok, mas o que esta análise nos diz sobre a amostra de 30 valores de salários que utilizamos?
Mínimo: o menor salário é de R$ 1.139
Primeiro quartil - Q1 = R$ 1.625: esta faixa de valores entre o mínimo e o Q1, no nosso exemplo é R$ 1.139 a R$ 1.625, e representa os salários que estão entre os 25% mais baixos da amostra
Mediana: o valor central deste conjunto de salários é de R$ 1.866 e a média dos salários da amostra é de R$ 2.080
Terceiro quartil - Q3 = R$ 2.327: esta faixa de valores entre o Q3 e o máximo, no nosso exemplo é R$ 2.327 a R$ 3.207, e representa os salários que estão entre os 75% mais altos da amostra
Máximo: o maior salário é de R$ 3.207
E quanto aos demais valores que estão no boxplot, digo, R$ 100, R$ 3.603, R$ 3.771 e R$ 3.991?
Bem, de imediato salta aos olhos o outlier de R$ 100. Esse valor pode nos indicar uma realidade cruel, se considerarmos que está correto, mas nos remete a verificar se não algum problema na base de dados ou na ETL (Extract Transform and Load ou Extração, Transformação e Carga dos dados). A propósito, caso queira mais alguns detalhes sobre a ETL, há uma publicação neste mesmo blog DataRoma. Este raciocínio aplica-se também aos outliers acima do valor máximo identificado.
Uma vez que os outliers tenham sido analisados e eventualmente tratado/corrigidos, quando for o caso, podemos concentrar nossa análise apenas nos quartis. E de que forma? Bem, aqui entra a natureza do que está sendo analisado ou a estratégia que tenha sido adotada.
Exemplificando, suponha que você esteja analisando qual é o salário que poderia oferecer a determinado profissional que deseja contratar. Nessa situação exemplo, se oferecêssemos um salário entre Q1 e Q3, estaríamos entre a maior parte dos valores praticados pelo mercado. Por outro lado, caso esse profissional seja muito demandado, oferecer um salário próximo ao quartil superior ou acima de Q3, tornaria sua vaga mais atrativa.
Concluindo
Via de regra, quando falamos de cálculos estatísticos as pessoas sentem sempre algum tipo de receio de que se trata de algo complexo e difícil. Neste post, tentei mostrar que o boxplot pode ser facilmente obtido com dois ou três cliques sobre os seus dados utilizando-se o MS-Excel.
Outras formas de obtê-lo e suas fórmulas podem até parecer mais complexas, mas não necessariamente você precisa se aprofundar em todos esses detalhes. Se compreender o significado dos quartis e como interpretá-los, pode confiar a sua obtenção à ferramenta estiver disponível. O MS Excel, por exemplo.
Saiba +
Consulte nos links a seguir mais detalhes sobre como criar e interpretar o boxplot, além de outros temas correlatos: